Raíz cuadrada

Expresión matemática de "raíz cuadrada de
X".
En las
ciencias matemáticas, se llama
raíz cuadrada de un número a cualquier otro número que elevado al
cuadrado, es igual al primero con esta definición cada
número complejo admite exactamente dos raíces cuadradas (estas son iguales en
módulo). A veces se abrevia como
raíz, siendo su símbolo:

. Es la
radicación de índice 2 o, equivalentemente, la
potenciación
con exponente ½. El concepto de raíz cuadrada puede extenderse a
cualquier anillo algebraico, así es posible definir la raíz cuadrada de
algunas matrices. En los
números cuaterniónicos
los reales negativos admiten un número infinito de raíces cuadradas,
sin embargo el resto de cuaterniones diferentes de cero admiten sólo dos
raíces cuadradas.
Función raíz cuadrada
La raíz cuadrada permite definir una función real sobre los números no negativos, para cada
número real x esta función se define como el único número no negativo
y que elevado al cuadrado es igual a
x. Consiste en hallar el número del que se conoce su cuadrado. La función raíz cuadrada de
x se expresa equivalente de las siguientes maneras:

Usualmente la raíz cuadrada de un número entero no es un número racional a menos que el número entero sea un
cuadrado perfecto, como por ejemplo:

ya que:

El descubrimiento de que la raíz cuadrada de muchos números era un
número irracional se atribuye a los
pitagóricos.
Los babilonios y egipcios ya disponían de medios de estimar
numéricamente la raíz cuadrada, pero su interés parece haber sido
eminentemente práctico por lo que no parecen existir referencias sobre
la naturaleza de la raíz cuadrada y el problema de si esta podía ser
expresada como cociente de dos números enteros.
Propiedades generales

Gráfica de la ecuación:

La función
raíz cuadrada 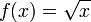
es una
función cuyo dominio e imagen es el conjunto

(el conjunto de todos los números reales no negativos). Esta función
regresa un valor que es único. Las siguientes propiedades de la raíz
cuadrada son válidas para todos los
números reales no negativos
x,
y:
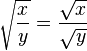

- La función raíz cuadrada, en general, transforma números racionales en números algebraicos;
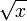 es racional si y sólo si
es racional si y sólo si  es un número racional que puede escribirse como fracción de dos cuadrados perfectos. Si el denominador es
es un número racional que puede escribirse como fracción de dos cuadrados perfectos. Si el denominador es 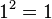 , entonces se trata de un número natural. Sin embargo,
, entonces se trata de un número natural. Sin embargo,  es irracional.
es irracional.
- La interpretación geométrica es que la función raíz cuadrada transforma la superficie de un cuadrado en la longitud de su lado.
- Contrariamente a la creencia popular,
 no necesariamente es igual a
no necesariamente es igual a  . La igualdad se mantiene sólo para los números no negativos
. La igualdad se mantiene sólo para los números no negativos  , pero cuando
, pero cuando 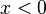 ,
,  es un número positivo, y entonces
es un número positivo, y entonces  . Por lo tanto,
. Por lo tanto,  para todos los números reales
para todos los números reales  (véase valor absoluto).
(véase valor absoluto).
- Suponga que
 y
y  son números reales, y que
son números reales, y que  , y se desea encontrar
, y se desea encontrar  . Un error muy común es "tomar la raíz cuadrada" y deducir que
. Un error muy común es "tomar la raíz cuadrada" y deducir que  . Esto es incorrecto, porque la raíz cuadrada de
. Esto es incorrecto, porque la raíz cuadrada de  no es
no es  , sino el valor absoluto
, sino el valor absoluto  , una de las reglas descritas anteriormente. Luego entonces, todo lo que se puede concluir es que
, una de las reglas descritas anteriormente. Luego entonces, todo lo que se puede concluir es que  , o equivalentemente
, o equivalentemente 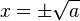 .
.
- En cálculo, cuando se prueba que la función raíz cuadrada es continua o derivable, o cuando se calculan ciertos límites, la siguiente igualdad es muy útil (consiste en multiplicar y dividir por el conjugado, véase Binomio conjugado):

- y es válida para todos los números no negativos
 e
e  que no sean ambos cero.
que no sean ambos cero.
- La función
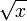 es continua para todos los números no negativos
es continua para todos los números no negativos  y derivable para todos los números positivos
y derivable para todos los números positivos  (no es derivable para
(no es derivable para  ya que la pendiente de la tangente ahí es ∞). Su derivada está dada por
ya que la pendiente de la tangente ahí es ∞). Su derivada está dada por

 . Es la radicación de índice 2 o, equivalentemente, la potenciación
con exponente ½. El concepto de raíz cuadrada puede extenderse a
cualquier anillo algebraico, así es posible definir la raíz cuadrada de
algunas matrices. En los números cuaterniónicos
los reales negativos admiten un número infinito de raíces cuadradas,
sin embargo el resto de cuaterniones diferentes de cero admiten sólo dos
raíces cuadradas.
. Es la radicación de índice 2 o, equivalentemente, la potenciación
con exponente ½. El concepto de raíz cuadrada puede extenderse a
cualquier anillo algebraico, así es posible definir la raíz cuadrada de
algunas matrices. En los números cuaterniónicos
los reales negativos admiten un número infinito de raíces cuadradas,
sin embargo el resto de cuaterniones diferentes de cero admiten sólo dos
raíces cuadradas.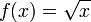 es una función cuyo dominio e imagen es el conjunto
es una función cuyo dominio e imagen es el conjunto  (el conjunto de todos los números reales no negativos). Esta función
regresa un valor que es único. Las siguientes propiedades de la raíz
cuadrada son válidas para todos los números reales no negativos x, y:
(el conjunto de todos los números reales no negativos). Esta función
regresa un valor que es único. Las siguientes propiedades de la raíz
cuadrada son válidas para todos los números reales no negativos x, y: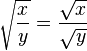

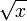 es racional si y sólo si
es racional si y sólo si  es un número racional que puede escribirse como fracción de dos cuadrados perfectos. Si el denominador es
es un número racional que puede escribirse como fracción de dos cuadrados perfectos. Si el denominador es 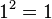 , entonces se trata de un número natural. Sin embargo,
, entonces se trata de un número natural. Sin embargo,  es irracional.
es irracional. no necesariamente es igual a
no necesariamente es igual a  . La igualdad se mantiene sólo para los números no negativos
. La igualdad se mantiene sólo para los números no negativos  , pero cuando
, pero cuando 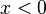 ,
,  es un número positivo, y entonces
es un número positivo, y entonces  . Por lo tanto,
. Por lo tanto,  para todos los números reales
para todos los números reales  (véase valor absoluto).
(véase valor absoluto). y
y  son números reales, y que
son números reales, y que  , y se desea encontrar
, y se desea encontrar  . Un error muy común es "tomar la raíz cuadrada" y deducir que
. Un error muy común es "tomar la raíz cuadrada" y deducir que  . Esto es incorrecto, porque la raíz cuadrada de
. Esto es incorrecto, porque la raíz cuadrada de  no es
no es  , sino el valor absoluto
, sino el valor absoluto  , una de las reglas descritas anteriormente. Luego entonces, todo lo que se puede concluir es que
, una de las reglas descritas anteriormente. Luego entonces, todo lo que se puede concluir es que  , o equivalentemente
, o equivalentemente 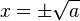 .
.
 e
e  que no sean ambos cero.
que no sean ambos cero.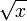 es continua para todos los números no negativos
es continua para todos los números no negativos  y derivable para todos los números positivos
y derivable para todos los números positivos  (no es derivable para
(no es derivable para  ya que la pendiente de la tangente ahí es ∞). Su derivada está dada por
ya que la pendiente de la tangente ahí es ∞). Su derivada está dada por en torno a
en torno a  se pueden encontrar usando el Teorema del binomio:
se pueden encontrar usando el Teorema del binomio:

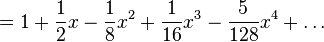
 .
.

 es una semi
es una semi




